
문제 풀 때마다 까먹어서 이항계수를 정리해보려 한다.
이항계수 nCr 은 n개중 r개를 선택하는 경우의 수를 의미하며 n!/r!(n-r!)로 나타낼 수 있다
알고리즘에서 이항계수를 구할 때 팩토리얼로 일일히 이항계수를 구하면 int범위를 벗어나 오버플로우가 발생하는 경우가 많다. 따라서 BigInteger를 이용해줄 수 있지만 보통은 재귀를 이용한다.
재귀를 이용할 때에도 시간초과가 날 수 있기 때문에 dp로 풀어주는 것이 일반적이다.
이항계수에는 중요한 규칙 두 가지가 있다.
1.nCr = n-1Cr + n-1Cr-1
2.nC0 = nCn = 1
이를 증명해보자
{a1,a2,a3....an}의 부분집합 중 원소의 개수가 r인 것의 개수는 nCr이다
여기서 원소의 개수가 r인 경우는 두가지로 나뉠 수 있다.
a1을 포함하는 원소r개인 부분집합의 개수 n-1Cr-1개
+
a1을 포함하지 않는 원소가 r개인 부분집합의 개수 n-1Cr-1개
따라서 n-1Cr-1 + n-1Cr = nCr이 된다.
또 n개 중 0개를 선택하는 경우의 수는 1가지이고, n개중 n개를 선택하는 경우의 수도 1가지 이므로
nCn = nC0 =1이된다
이 규칙을 이용하여 다음과 같이 이항계수를 구하는 함수를 만들 수 있다.
static int bc(int N, int K){
if(K==0||N==K) return 1; //nCn이거나 nC0인경우 1리턴
else if(dp[N][K]!=0) return dp[N][K];
return dp[N][K] = (eg(N-1,K-1)+eg(N-1,K));//1.nCr = n-1Cr + n-1Cr-1
}
이항 계수를 이용하여 다음 두 문제를 풀 수 있다.
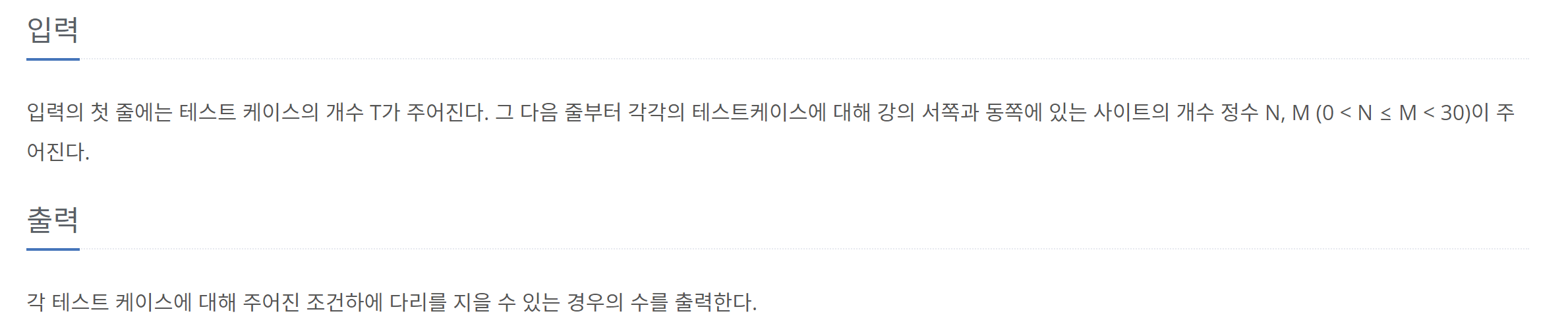
백준 1010 -다리놓기

public class Baek_1010 {
static int[][] dp = new int[31][31];
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int tc = Integer.parseInt(br.readLine());
StringBuilder sb = new StringBuilder();
while (tc-- > 0) {
StringTokenizer st = new StringTokenizer(br.readLine(), " ");
int n = Integer.parseInt(st.nextToken());
int m = Integer.parseInt(st.nextToken());
sb.append(bridge(n, m)).append("\n");
}
System.out.println(sb);
}
static int bridge(int n, int m) {
if (n == m || n == 0) return 1;
else if(dp[m][n]!=0) return dp[m][n];
return dp[m][n] = bridge(n - 1, m - 1) + bridge(n, m - 1);
}
}
이 문제를 BigInteger를 이용해서도 풀어보았다. 이때는 factorial값을 dp에 저장해주었다
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.math.BigInteger;
import java.util.StringTokenizer;
public class Main {
static BigInteger[] dp = new BigInteger[31];
public static void main(String[] args) throws IOException {
BufferedReader br= new BufferedReader(new InputStreamReader(System.in));
int tc = Integer.parseInt(br.readLine());
StringBuilder sb = new StringBuilder();
dp[1] = BigInteger.valueOf(1);
//dp[n] = n*dp[n-1]
while (tc-->0) {
StringTokenizer st = new StringTokenizer(br.readLine(), " ");
int n = Integer.parseInt(st.nextToken());
int m = Integer.parseInt(st.nextToken());
sb.append(bridge(n,m)).append("\n");
}
System.out.println(sb);
}
static BigInteger bridge(int n, int m){
if(n==m) return BigInteger.valueOf(1);
return factorial(m).divide(factorial(n).multiply(factorial(m-n)));
}
static BigInteger factorial(int num){
if(dp[num]!=null) return dp[num];
return dp[num] = BigInteger.valueOf(num).multiply(factorial(num-1));
}
}두 방법의 메모리사용량과 시간은 다음과 같다.
bc공식을 이용한 방식

BigInteger를 이용한 방식

위 문제의 경우에는 BigInteger가 더 빠르긴 한데 웬만하면 공식 이용해서 푸는게 코드도 깔끔하고 좋을 것 같다.
백준 11051 - 이항계수 2

import java.io.IOException;
import java.util.Scanner;
//이항계수 2
public class Baek_11051 {
static int[][] dp;
public static void main(String[] args) throws IOException {
Scanner sc = new Scanner(System.in);
int N = sc.nextInt();
int K = sc.nextInt();
dp = new int[N+1][N+1];
System.out.println(eg(N,K));
}
static int eg(int N, int K){
if(K==0||N==K) return 1;
else if(dp[N][K]!=0) return dp[N][K];
return dp[N][K] = (eg(N-1,K-1)+eg(N-1,K))%10007;
}
}'Algorithm' 카테고리의 다른 글
| 백준 1041 주사위 (3) | 2023.05.04 |
|---|---|
| 백준 1663 -XYZ 문자열 (1) | 2023.05.03 |
| [JAVA] DFS,재귀 이해하기/ 백준 2644 촌수계산 (1) | 2023.05.01 |
| [모듈러 연산] 백준 11726 /프로그래머스 - 피보나치 수 (0) | 2023.04.21 |
| [Java]Quick Sort (2) | 2023.04.21 |