
문제

입출력 예시
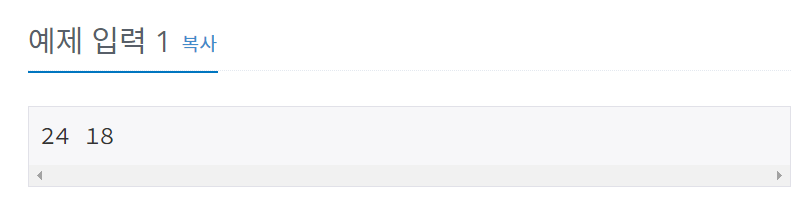

처음 풀이
처음에는 정말 최대공약수와 최소공배수 구하는 공식 그대로 생각해서 구현해서 풀었다.
import java.util.Scanner;
//최대공약수와 최소공배수
public class Baek_2609 {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int num1 = in.nextInt();
int num2 = in.nextInt();
int commonDivisor = 1; //최초 최대공약수 1로 설정
//두 수중 작은 수에서부터 돌면서 공약수를 확인
for (int i = Math.min(num1, num2); i > 1; i--) {
/*만약 i가 num1과 num2의 공약수이면*/
if (num1 % i == 0 && num2 % i == 0) {
commonDivisor *= i; // 최대공약수 변수에 i값 곱해줌
num1 /= i;
num2 /= i; //num1과 num2값은 i로 나눠진 상태에서 다시 for문을 돌 것
}
}
int commonMultiple = commonDivisor*num1*num2; //최소공배수 = 최대공약수 * 나눠진수1*나눠진수2
System.out.println(commonDivisor+ "\n" + commonMultiple);
}
}
이렇게 풀면 코드가 길어져서 가독성이 떨어질 수 있다.
그래서 스터디시간에 유클리드 호제법을 통해 푸는 법을 배웠다
(실은 찾아봤지만 이해하기 어려웠는데 스터디원분이 이해하기 쉽게 설명해주셨다.)
🔎유클리드 호제법
두 수 A와 B가 있을 때
A는 B에 어떤 수를 곱한 값 + 나머지(R)로 나타낼 수 있다.
다음과 같이 말이다.
A = B * Q + R
A와 B의 최대공약수를 G라 할 때
A와 B는 최대공약수 G와 어떤 수(a,b)의 곱으로 표현할 수 있다.
식으로 표현해보자
a*G = b*G*Q + R
이제 이 식을 R에 대한 식으로 이항해서 정리해보면
R = G(a-b*Q)
세상에.... R도 G(A와 B의 최대공약수)를 가진다!😮
따라서 유클리드 호제법에 의하면 A를 B로 나눈 나머지 R도 A와 B의 최대공약수 G를 가지게 된다.
재귀함수로 B와 R을 넘겨가면서 진행하여 최대공약수를 구해보자.
유클리드 호제법을 적용한 풀이
import java.util.*;
public class Baek_2609_2 {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int num1 = in.nextInt();
int num2 = in.nextInt();
int GCD = gcd(num1, num2);//최대공약수
int LCM = num1 * num2 / GCD; //최소공배수
System.out.println(GCD);
System.out.println(LCM);
}
//유클리드 호제법을 적용해 최대공약수를 구하는 메서드!
public static int gcd(int num1, int num2){
if (num1 % num2 == 0) return num2; // num1을 num2로 나눴을 때 나머지가 0이면 자연스레 최대공약수는 num2가 됨
return gcd(num2, num1 % num2); //num2로 바꾸고 num2를 R로 바꾼다.
}
}
최소공배수는
최대공약수 * num1/최대공약수 * num2/최대공약수
만 해주면 되므로 최대공약수를 구하고 나면 간단하게 구할 수 있다.
'Algorithm' 카테고리의 다른 글
| 분할 정복 정복하기~ (2) | 2023.04.20 |
|---|---|
| [DP]백준 9095 예제 뿌시기 (0) | 2023.04.14 |
| DFS / BFS (0) | 2023.04.14 |
| 백준 10814 - 나이순 정렬 JAVA (0) | 2022.11.19 |
| [데일리코딩] 피보나치, 메모이제이션 (0) | 2022.11.07 |