DFS와 BFS가 많이 헷갈려서 이해하기 가장 편했던 방식으로 정리해보려 한다.
정말정말 풀어서 썼기에 깔끔하게 핵심만 넣었다기 보단
DFS와 BFS를 처음 접하는 사람이 이것을 이해하는 과정을 상세하게 다 적었구나 생각하면 될 것 같다.
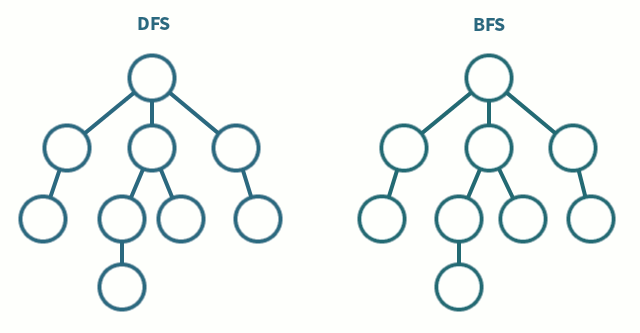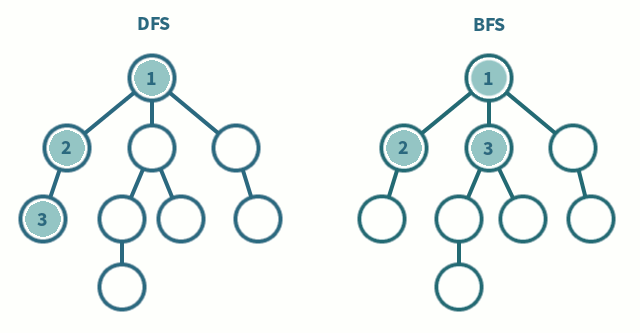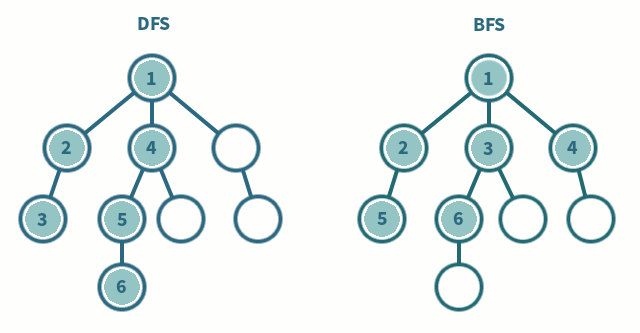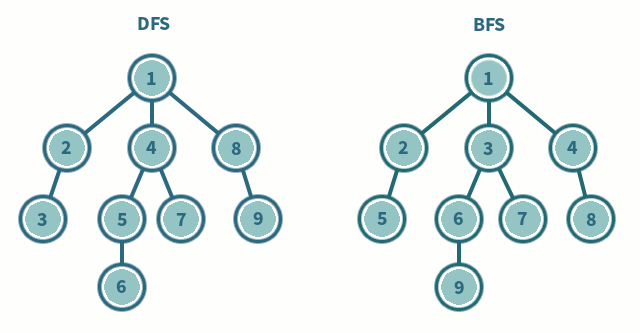
DFS vs. BFS
DFS는 깊이우선 탐색
BFS는 넓이 우선 탐색을 뜻한다.

깊이 우선 탐색은 말 그대로 정점에서 갈 수 있는 가장 먼(깊은) 점까지 들어가서 탐색하는 것이고,
넓이우선 탐색은 현재 정점에 연결된 가장 가까운 점들부터 탐색한다.
검색 속도는BFS가 빠르지만 DFS가 더 간단하다.
따라서 검색 대상 그래프가 크거나 경로의 특징을 저장해둬야 하는 문제는 DFS를,
검색 대상의 규모가 크지 않고 최단거리를 구해야 하는 문제는 BFS가 유리하다.
일상생활에서 접하기 쉬운 예로 생각해보자
나와 선영이가 가위 바위 보 게임을 3판 한다고 했을 때
내가 가위,바위,보를 낼 수 있는 모든 경우의 수를 어떻게 나열할 수 있을까?
1. DFS적 사고
가위 가위 가위
가위 가위 바위
가위 가위 보
가위 바위 가위
가위 바위 바위
.
.
.
DFS적 으로 생각해보면 이렇게 들어간다.
즉 가장 깊은 곳으로 들어가 자식리프들부터 탐색한다.
자세한 것은 뒤에 나오니 여기서 이해가 안된다면 이렇구나 정도만 짚고 넘어가도 괜찮다.
2.BFS적 사고
가위/x/x 9개
바위/x/x 9개
보/x/x 9개씩을 먼저 써놓고
두번째 라운드를 하나씩 써내려간다.
이런 방식이 BFS적 사고로 경우의 수를 작성하는 것이다.
구현과정
dfs는 보통 스택으로
bfs는 큐로 구현한다.
다음과 같은 Binary Tree가 있다고 가정해보자
0
1 2
3 4 5 6
1. DFS 탐색
가장 먼저, 루트인 0을 자료구조(스택)에 넣고
자료구조에 있는 노드를 빼서 그 노드의 자식노드를 넣어 탐색하는 과정으로 갈 것이다.
스택은 LIFO(Last In First Out)구조라는 것을 기억하자!
스택에는 0이 들어가고
스택 - [0 ] / 탐색순서-[]
0을 탐색하며 빠지며 0의 자식 노드인 1,2가 차례로 들어갈 것이다
스택[1,2] / 탐색순서 -[0]
마지막에 들어온 2를 탐색하며 빼주고 2의 자식 노드인 5 6이 차례로 들어갈 것이다.
스택[1,5,6] / 탐색순서 - [0,2]
6을 탐색하며 빼주는데 이때 6은 자식노드가 없다.
스택[1,5] / 탐색순서 - [0,2,6]
따라서 5를 탐색하며 빼주는데 5도 자식노드가 없다.
스택[1] / 탐색순서 - [0,2,6,5]
1을 탐색하며 빼주는데 이때 1은 3,4 자식노드를 가지고 있으므로 스택에 넣어준다.
스택[3,4] / 탐색순서 - [0,2,6,5,1]
3,4도 차례로 탐색하며 빼주는데 3,4는 자식 노드가 없으므로 빼주기만 하면 된다.
스택[] / 탐색순서 - [0,2,6,5,1,3,4]
더이상 스택에 노드가 없으므로 탐색이 끝낫다.
따라서 DFS방식으로 탐색을 했다면 탐색 순서는 0->2->6,5,1,3,4로
가장 아래의 자식 노드까지 들어가 탐색하게 된다.
이제 DFS를 Java코드로 구현해보겠다.
public class DFS {
public static void main(String[] args){
//각 노드가 연결된 정보를 2차원 배열 자료형으로 표현
int [][]graph = {{},
{2, 3, 8},
{1, 7},
{1, 4, 5},
{3, 5},
{3, 4},
{7},
{2, 6, 8},
{1, 7}};
//각 노드가 방문된 정보를 1차원 배열 자료형으로 표현
boolean [] visited = {false, false, false ,false ,false ,false ,false ,false, false};
//정의된 DFS 함수 호출
DFS_Stack dfsExam = new DFS_Stack();
dfsExam.dfs(graph, 1, visited);
}
/*
* dfs 메서드
* @param graph 노드 연결 정보를 저장
* @param v 방문을 시작하는 최상단 노드의 위치
* @param visited 노드 방문 정보를 저장
*/
void dfs(int [][]graph,int start, boolean [] visited){
//시작 노드를 방문 처리
visited[start] = true;
System.out.print(start + " ");//방문 노드 출력
Deque<Integer> stack = new LinkedList<>();
stack.push(start); //시작 노드를 스택에 입력
while(!stack.isEmpty()){
int now = stack.peek();
boolean hasNearNode = false; // 방문하지 않은 인접 노드가 있는지 확인
//인접한 노드를 방문하지 않았을 경우 스택에 넣고 방문처리
for(int i: graph[now]){
if (!visited[i]) {
hasNearNode = true;
stack.push(i);
visited[i] = true;
System.out.print(i + " ");//방문 노드 출력
break;
}
}
//반문하지 않은 인접 노드가 없는 경우 해당 노드 꺼내기
if(hasNearNode==false)
stack.pop();
}
}
}
1. BFS 탐색
import java.util.LinkedList;
import java.util.Queue;
public class BFS {
public static void main(String[] args){
//각 노드가 연결된 정보를 2차원 배열 자료형으로 표현
int [][]graph = {{},
{2, 3, 8},
{1, 7},
{1, 4, 5},
{3, 5},
{3, 4},
{7},
{2, 6, 8},
{1, 7}};
//각 노드가 방문된 정보를 1차원 배열 자료형으로 표현
boolean [] visited = {false, false, false ,false ,false ,false ,false ,false, false};
int start = 1; // 시작 노드
// 큐 구현
Queue<Integer> queue = new LinkedList<>();
queue.add(start);
// 현재 노드를 방문 처리
visited[start] = true;
// 큐가 빌때까지 반복
while(!queue.isEmpty()){
// 큐에서 하나의 원소를 뽑아 출력
int v = queue.poll();
System.out.println(v + " ");
// 인접한 노드 중 아직 방문하지 않은 원소들을 큐에 삽입
for (int i : graph[v]){
if (visited[i] == false){
queue.add(i);
visited[i] = true;
}
}
}
}
}'Java' 카테고리의 다른 글
| java- IEEE 754 부동 소수점 방식 (1) | 2023.02.02 |
|---|---|
| Java - Scanner vs. BufferedReader (1) | 2022.10.03 |
| Java- StringBuilder의 메소드 (1) | 2022.09.26 |
| Java - split()/join() 배열<->문자열 변환 (1) | 2022.09.23 |
| Java - 많이 쓰는 메소드 정리1 (배열 복사) (0) | 2022.09.23 |